黎曼猜想-素数-RSA-非对称加密-https-通信安全

#一句话总结：

素数的出现频率与黎曼 ζ 函数密切相关。 如果随机选择一个自然数x，则P(x)，即该数是质数的概率约为1/ln(x)，看来对RSA非对称加密没有破坏作用，来解密或者需要蛮力

黎曼猜想

黎曼 zeta 函数，

{\displaystyle \zeta (s)={\frac {1}{1^{s}}}+{\frac {1}{2^{s}}}+{\frac {1}{3^{s }}}+{\frac {1}{4^{s}}}+\cdots }

.

黎曼 zeta 函数的非平凡零的实部是 ½

也就是说，所有非平凡零点都应该位于 {\displaystyle {\frac {1}{2}}+t\mathbf {i} }

（“临界线”）。 _t_是实数，i是虚数的基本单位。

图像示意图

您可以在文末观看相应的视频

黎曼素数计数函数

黎曼用π(x)定义了自己的素数计数函数，即黎曼素数计数函数J(x)。 它被定义为：

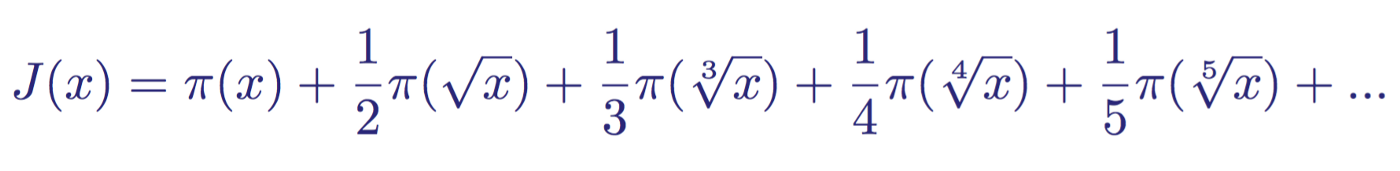
来源：()https://zhuanlan.zhihu.com/p/25222934

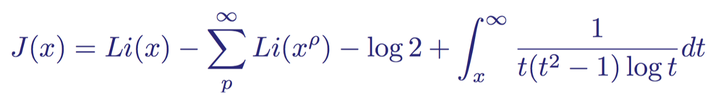
“黎曼素数定理”猜出的给定数x内的素数个数

这是黎曼的显式。 它是对素数定理的改进，可以更准确地估计出x及以上的数中存在多少个素数。 该公式有四项：

第一项，或称“主项”，是对数积分 Li(x)，它是素数定理对素数计数函数 π(x) 的更好估计。 它是迄今为止最大的一项，正如我们之前看到的，它高估了有多少素数包含给定值 x。

第二项，或“周期项”，是 ρ 的对数积分的总和提高到 x 的 ρ 次方（原始数字被误认为是 p，感谢

@爱迪儿

校正），它是 zeta 函数的非平凡零。 它用于调整主项的高估项。

第三项是常数 -log(2) = -0.6993147...

第四项也是最后一项是在 x < 2 上为零的积分，因为没有小于 2 的素数。当积分约等于 0.1400101... 时，它的最大值为 2。

随着这个函数值的增加，后两项的贡献是无穷小的。 大数的主要“贡献者”是对数积分和周期和。

黎曼一举揭开了素数最深奥的秘密，优雅地给出了素数分布的精确表达式。 人们第一次能够近距离观察自然界中质数舞动的规律。 就是那样的奔放，不羁。 平静时，如温柔的月光洒在波涛汹涌的大海上，汹涌时，又如巨浪倾泻在孤舟上。 爱恨交织，眼神动人。

但是，素数并不是完全随机的，它的表现总是服从黎曼zeta函数零点的分布规律。

素数

素数，又称素数，是指大于1的数，除1和数本身外，不能被其他自然数整除（也可定义为只有1和2个正因数的数）数字本身）。 大于1且不是质数的自然数称为合数（也称合数）。

素数定理

素数定理也由高斯（和勒让德独立地）制定：

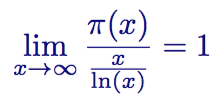
素数定理

中文（英文原文）是这样表述的：“当 x 增长到无穷大时，素数计数函数 π(x) 将逼近 x/ln(x) 函数。换句话说，如果你的计数足够大，并且绘制最大数 x 的素数个数，然后绘制 x 除以 x 的自然对数，两者将趋近于相同的值。

素数的随机性带来了很大的应用

素数的应用

长期以来，数论，尤其是素数的研究，一般被认为是典型的纯数学，除了求知的兴趣外，没有其他应用。 特别是，一些数论学家，如英国数学家戈弗雷哈代，以他们的工作从来没有任何军事重要性而自豪 [44]。 然而，这种观点在 1970 年代被打破，当时公开宣布素数是生成公钥​​加密算法的基础。 素数现在也用于哈希表和伪随机数生成器。

旋转电机设计为在每个转子上具有不同数量的销钉，并且每个转子上的销钉数量将与其他转子上的销钉数量互质或互质。 这有助于在重复所有组合之前让所有可能的旋转组合出现一次。

ISBN 的最后一个代码是校验位，其算法利用了 11 是质数这一事实。

在设计上，相邻两个大小齿轮的齿数应设计成质数成功暴力破解比特币私钥，以增加两个齿轮中两个相同齿相交啮合次数的最小公倍数，可增强耐用性并减少失败。

质数农药的使用在害虫的生物生长周期与农药使用的关系中也得到了证明。 实验证明，质数使用杀虫剂最合理：都是在害虫繁殖高峰期使用，害虫很难产生抗药性[来源请求]。

以质数形式随机变化的导弹和鱼雷会使敌人难以拦截 [来源请求]。

RSA加密与素数关系

简单的说，RSA加密的前提是：大整数的因式分解是一件非常困难的事情。 目前除了暴力破解外，还没有找到其他有效的方法。

回顾上面的密钥生成步骤，一共有六个数字：

pqnφ(n) ed

在这六个数字中，两个（n和e）用于公钥，其余四个数字不公开。 最关键的是d，因为n和d组成了私钥，d一旦泄露，就等于私钥泄露了。

那么，是否有可能在给定 n 和 e 的情况下推导出 d？

（1）ed≡1 (mod φ(n))。只有知道e和φ(n)，才能算出d。

(2) φ(n)=(p-1)(q-1)。 只有知道 p 和 q 才能计算出 φ(n)。

(3) n=pq。 只有对 n 进行因式分解，才能计算出 p 和 q。

结论：如果n可以因式分解，就可以计算出d，说明私钥被破解了。

然而，大整数的因式分解是一件非常困难的事情。 目前除了暴力破解外，还没有找到其他有效的方法。 维基百科写道：

“分解一个非常大的整数的难度决定了RSA算法的可靠性。换句话说，分解一个非常大的整数越困难，RSA算法就越可靠。

如果有人找到快速分解的算法，RSA 的可靠性将大大降低。 但是找到这样一种算法的机会非常渺茫。 今天只有短的 RSA 密钥可以被暴力破解。 截至2008年，世界上还没有可靠的方法可以攻击RSA算法。

只要密钥长度足够长，用RSA加密的信息实际上是无法被破解的。 “

公私钥生成过程：

假设 Alice 想通过不可靠的媒介接收 Bob 的私人消息。 她可以通过以下方式生成公钥和私钥：

随机选择两个大质数p_和_q，p_不等于_q，计算_N_=pq。 根据欧拉函数，得到r = (p-1)(q-1) 选择一个小于r的整数_e_，得到e对模r的逆元，命名为d。 （成型元素存在，当且仅当e和r互质）销毁_p和q_的记录。

_(N,e) 是公钥，(N,d)_ 是私钥。 Alice 将她的公钥 (N,e) 传递给 Bob，但隐藏了她的私钥 (N,d)。

RSA算法原理及其在HTTPS中的应用

数字证书原理

RSA在生成公钥和私钥时如何选择素数？

1.素数的个数

前x个正整数中约有x/lnx个素数，即随机选取一个自然数x，则P(x)成功暴力破解比特币私钥，即该数为素数的概率约为1/ln( X）

2、如何判断一个数是否为质数？

3.如何选择素数？

比特币背后的密码学

比特币系统中实际使用的非对称算法是椭圆曲线密码学（ECC），可以在这里详细了解。

从上面的例子我们知道存在满足非对称加密的密钥对，我们也尝试过加解密。 事实上，非对称加密算法的核心取决于一个具体的数学问题。 例如，上面的 RSA 依赖于大数分解问题。 如果问题解决了，算法本身就坏了。

非对称算法通过公钥和私钥的加解密方式，给信息交换带来了巨大的变化，具体表现在：

1）在不安全的环境中传输敏感信息成为可能。 由上可知，公钥是完全公开和自由传播的。 通过公钥计算出私钥是不可能的（或极其困难的）。 没有其他人需要知道。

2) 多方通信所需的密钥数量大幅减少，密钥维护变得极其简单。 比如N个人互不信任，需要互相交流，如果采用对称加密算法，N！ /2个密钥，如果使用非对称加密，只需要N个（每个人只需要维护自己的公私对，不管与多少人通信）。

3）基于非对称加密（详见下文）发展起来的数字签名技术，从数学意义上解决了自我证明的问题，使信息接收方可以确认消息发送方的身份信息，不可更改。

4）密码学问题对数学问题的依赖程度从未如此之高。 以前看似无用甚至古老的数学问题，例如数论和离散对数，在这里大放异彩。 颇有几分反映了老师在《把时间当朋友》中所表达的“技不压身”的现实。

所谓数字签名，是指签名者用自己的私钥对签名数据的摘要进行加密得到的值就是签名值。 签名者在发送数据签名时，需要将待签名的数据和签名值发送给对方。

注意签名对象不是待签名数据而是待签名数据的摘要，为什么呢？ 因为非对称加密的速度通常比较慢，直接对原始数据的私钥进行加密非常慢，没有必要。

如何验证签名？ 接收方先用签名者的公钥解密签名值得到摘要值，然后用约定的算法对签名后的数据进行哈希处理，与解密后的摘要值进行比较验证。

挖矿的具体实现是在一定难度下，通过暴力双SHA256哈希运算，获取满足难度目标的Nonce值。 所谓工作量证明，就是对无数次哈希运算进行穷举和比较的过程。